This paper considers the ergodicity of maps on the two-dimensional torus, focusing on transformations where invariant real-valued functions are constant. The study considers both additive and multiplicative transformations, providing a detailed analysis of the conditions required for a map to be classified as ergodic. The investigation is grounded in the theory of dynamical systems and leverages mathematical tools such as orthonormal double sequences in Hilbert spaces and Fourier series to establish necessary and sufficient conditions for ergodicity. By connecting these conditions to the Lebesgue measure, the research outlines the fundamental properties of ergodic transformations on the torus. A key aspect of this study is its treatment of invariant functions and their role in defining ergodic behavior. Invariant functions, which remain unchanged under the dynamics of a given transformation, are examined in depth to understand how their constancy relates to the overall system. The analysis also highlights the interplay between additive and multiplicative transformations and their impact on the ergodic properties of the system. The results of this work not only provide a robust framework for understanding the dynamics of transformations on the two-dimensional torus but also have implications for higher-dimensional systems. This contribution is particularly relevant for studying complex systems in ergodic theory, where the behavior of transformations under the Lebesgue measure often serves as a foundation for further exploration. By addressing these fundamental aspects, the paper lays the groundwork for extending these concepts to more intricate and multidimensional settings in mathematical and applied research.
| Published in | International Journal of Systems Science and Applied Mathematics (Volume 10, Issue 1) |
| DOI | 10.11648/j.ijssam.20251001.11 |
| Page(s) | 1-6 |
| Creative Commons |
This is an Open Access article, distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution and reproduction in any medium or format, provided the original work is properly cited. |
| Copyright |
Copyright © The Author(s), 2025. Published by Science Publishing Group |
Ergodic Theory, Two-Dimensional Torus, Invariant Functions, Fourier Series, Lebesgue Measure
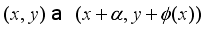 on the torus
on the torus 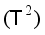 , where
, where  is irrational, has the same spectral type as the cross-product of the shift transformation on an infinite torus. However, while the induced operators in
is irrational, has the same spectral type as the cross-product of the shift transformation on an infinite torus. However, while the induced operators in 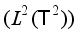 are unitarily equivalent, the transformations are not isomorphic.
are unitarily equivalent, the transformations are not isomorphic. 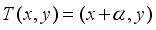 is given for
is given for 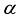 irrational, where
irrational, where 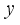 is a measurable function. The condition for non-ergodicity in this case is that there exists an integer
is a measurable function. The condition for non-ergodicity in this case is that there exists an integer 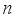 and a measurable map g such that
and a measurable map g such that 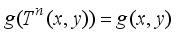 almost everywhere. This condition provides a basis for analyzing non-ergodicity in skew-product systems.
almost everywhere. This condition provides a basis for analyzing non-ergodicity in skew-product systems. 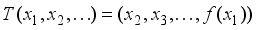 , where
, where 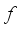 represents the skewing function. These transformations are closely linked to representations of groups and serve as valuable tools for understanding the structure of complex dynamical systems
represents the skewing function. These transformations are closely linked to representations of groups and serve as valuable tools for understanding the structure of complex dynamical systems 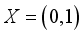 and let
and let 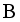 be the σ-algebra of all Lebesgue measurable subsets of X. Suppose that
be the σ-algebra of all Lebesgue measurable subsets of X. Suppose that 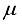 is
is 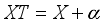 mod
mod 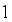 where
where  is irrational. Here
is irrational. Here 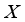 is locally compact (but not compact), however is Hausdorff subspace of the real line
is locally compact (but not compact), however is Hausdorff subspace of the real line 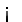
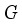 be the circle group, that is, the topological group of all complex numbers
be the circle group, that is, the topological group of all complex numbers 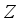 with absolute value 1 equipped with the normalized Haar measure
with absolute value 1 equipped with the normalized Haar measure 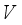 on
on 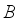 (
( 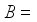 the o-algebra of all Borel subset of
the o-algebra of all Borel subset of 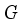 ) then, the map
) then, the map 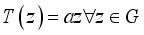 , where
, where 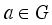 is not a root of unity
is not a root of unity 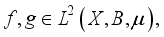 then
then 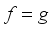 holds, and
holds, and 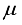 is almost everywhere, if and only if, their Fourier coefficients are equal i.e.
is almost everywhere, if and only if, their Fourier coefficients are equal i.e. 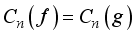
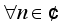 (1)
(1) 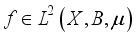 , then we associate with
, then we associate with 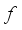 the FS.
the FS. 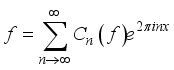 (2)
(2) 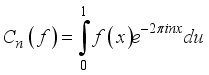 (3)
(3) 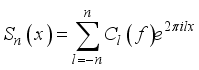 (4)
(4) 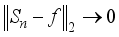 as
as 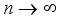 .
. 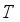 is measure preserving transformation it follows that
is measure preserving transformation it follows that 
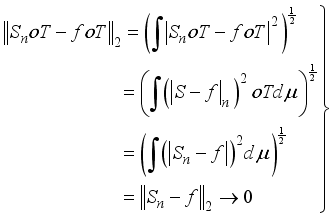 (5)
(5) 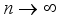 , it follows that the
, it follows that the 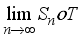 is the possible sum of the form
is the possible sum of the form 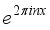 , which gave FS of
, which gave FS of 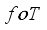 .
. 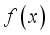 and evaluate at
and evaluate at 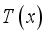 , then we obtain the FS
, then we obtain the FS 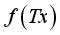 . i.e
. i.e  (6)
(6) 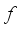 is constant
is constant 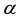 be irrational and let
be irrational and let 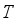 be the mapping of the two dimensional tours
be the mapping of the two dimensional tours 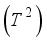 in mod 1 given by the formula.
in mod 1 given by the formula. 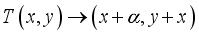 ,(7)
,(7) 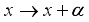 on
on 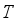 as the base and
as the base and 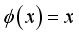 (8)
(8) 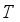 is ergodic on
is ergodic on 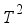 with respect to the lebsegue measure.
with respect to the lebsegue measure. 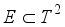 be some Borel set with
be some Borel set with 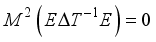 (9)
(9) 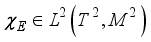 ,
, 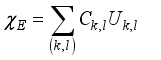 (10)
(10) 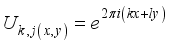 (11)
(11) 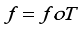 (12)
(12) 
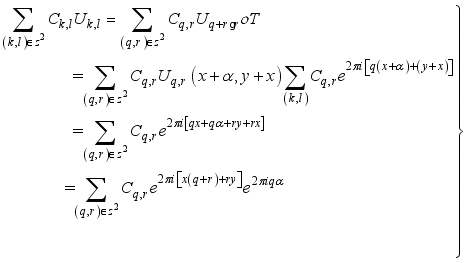 (13)
(13) 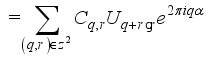 (14)
(14) 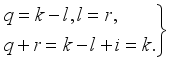 (15)
(15) 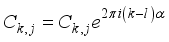 (16)
(16) 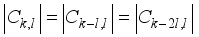 (17)
(17) 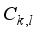 is the square sum on
is the square sum on  then
then 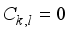 , whenever
, whenever 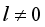 .
. 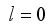 , we have
, we have 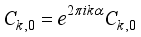 (18)
(18) 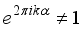
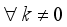 ,
, 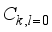 for all
for all 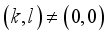 .
. 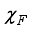 is an arbitrary constant on
is an arbitrary constant on 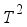 , which shows that it is an ergodic.
, which shows that it is an ergodic. 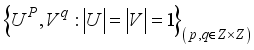 and
and 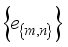 be a complete orthonormal double sequence in Hilbert space H,
be a complete orthonormal double sequence in Hilbert space H, 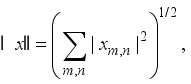 where ∥x∥ is the norm induced by the inner product, and
where ∥x∥ is the norm induced by the inner product, and 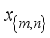 are the coefficients corresponding to the orthonormal basis
are the coefficients corresponding to the orthonormal basis 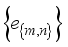
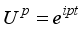 and
and 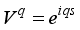 (19)
(19) 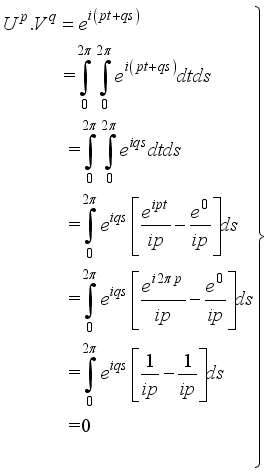 (20)
(20) 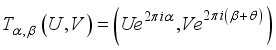 (21)
(21) 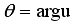 , where
, where 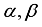 are irrational real constants, for all complex
are irrational real constants, for all complex 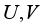 , then
, then 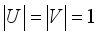 is ergodic
is ergodic 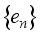 be a complete orthonormal double sequence in Hilbert space H in Hilbert space
be a complete orthonormal double sequence in Hilbert space H in Hilbert space 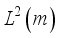 . If f is a function in H, i.e
. If f is a function in H, i.e 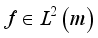 , then
, then 
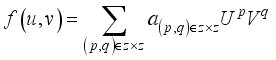 ,(22)
,(22) 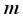 for some constants
for some constants  , called the Fourier coefficient with respect to orthonormal sequence
, called the Fourier coefficient with respect to orthonormal sequence 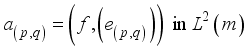
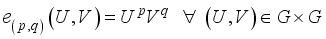 (23)
(23) 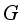 is a circle group. Hence,
is a circle group. Hence, 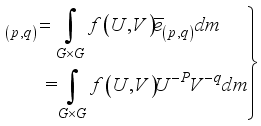 ,(24)
,(24)  .
. 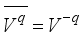 .
. 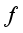 is
is 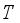 -invariant function in
-invariant function in 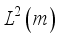 , then
, then  (25)
(25)  ,(26)
,(26)  .
.  .
. 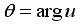 ,
, 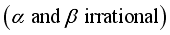 .
. 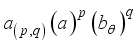 .
. 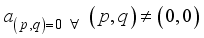 .
. 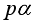 is not an integer, except
is not an integer, except 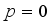 and
and 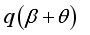 is not an integer except q=0. Then for
is not an integer except q=0. Then for 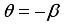 . Thus
. Thus 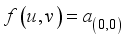 ,
, 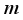 in
in 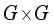 .
. ET | Ergodic Theory |
FS | Fourier Series |
LM | Lebesgue Measure |
| [1] | Hawkins, J. (2021). Ergodic dynamics. Springer International Publishing. |
| [2] | Nicol, M., & Petersen, K. (2023). Ergodic theory: Basic examples and constructions. In Ergodic theory (pp. 3–34). New York, NY: Springer US. |
| [3] | Barreira, L., & Pesin, Y. (2023). Introduction to smooth ergodic theory (Vol. 231). American Mathematical Society. |
| [4] | Frantzikinakis, N., & McCutcheon, R. (2023). Ergodic theory: Recurrence. In Ergodic theory (pp. 61–78). New York, NY: Springer US. |
| [5] | del Junco, A. (2023). Ergodic theorems. In Ergodic theory (pp. 79–107). New York, NY: Springer US. |
| [6] | Buzzi, J. (2023). Chaos and ergodic theory. In Ergodic theory (pp. 633–664). New York, NY: Springer US. |
| [7] | Aravinda, C. S., & Bhat, V. S. (2022). Basic ergodic theory. In Elements of dynamical systems: Lecture notes from NCM School (pp. 73–107). Singapore: Springer Nature Singapore. |
| [8] | Adams, T., & Quas, A. (2023). Ergodicity and mixing properties. In Ergodic theory (pp. 35–60). New York, NY: Springer US. |
| [9] | Damanik, D., & Fillman, J. (2022). One-dimensional ergodic Schrödinger operators: I. General theory (Vol. 221). American Mathematical Society. |
| [10] | Cohen, G., & Lin, M. (2023). Uniform ergodicity and the one-sided ergodic Hilbert transform. arXiv preprint arXiv: 2310.15561. |
| [11] | Okubo, K. I., & Umeno, K. (2021). Infinite ergodicity that preserves the Lebesgue measure. Chaos: An Interdisciplinary Journal of Nonlinear Science, 31(3). |
| [12] | Sambarino, A. (2024). A report on an ergodic dichotomy. Ergodic Theory and Dynamical Systems, 44(1), 236–289. |
| [13] | Silva, A. F. D. (2023). Contributions to phase transition of intermittent skew-product and piecewise monotone dynamics on the circle. |
| [14] | Liu, N., & Liu, X. (2024). On the variational principle for a class of skew product transformations. arXiv preprint arXiv: 2406.16883. |
| [15] | Danilenko, A. I., & Silva, C. E. (2023). Ergodic theory: Nonsingular transformations. In Ergodic theory (pp. 233–292). New York, NY: Springer US. |
| [16] | Clotet, S. B. (2022). Sorbonne Université (Doctoral dissertation, Université de Lorraine). |
| [17] | Yu, H. (2021). An improvement on Furstenberg’s intersection problem. Transactions of the American Mathematical Society, 374(9), 6583–6610. |
| [18] | Feldman, G. (2023). Characterization of probability distributions on locally compact Abelian groups (Vol. 273). American Mathematical Society. |
| [19] | Bruin, H. (2022). Topological and ergodic theory of symbolic dynamics (Vol. 228). American Mathematical Society. |
APA Style
Nduka, G. S., Egbogho, H. E. (2025). Ergodicity of Maps on the Two-Dimensional Torus. International Journal of Systems Science and Applied Mathematics, 10(1), 1-6. https://doi.org/10.11648/j.ijssam.20251001.11
ACS Style
Nduka, G. S.; Egbogho, H. E. Ergodicity of Maps on the Two-Dimensional Torus. Int. J. Syst. Sci. Appl. Math. 2025, 10(1), 1-6. doi: 10.11648/j.ijssam.20251001.11
AMA Style
Nduka GS, Egbogho HE. Ergodicity of Maps on the Two-Dimensional Torus. Int J Syst Sci Appl Math. 2025;10(1):1-6. doi: 10.11648/j.ijssam.20251001.11
@article{10.11648/j.ijssam.20251001.11,
author = {George Smart Nduka and Henry Etaroghene Egbogho},
title = {Ergodicity of Maps on the Two-Dimensional Torus
},
journal = {International Journal of Systems Science and Applied Mathematics},
volume = {10},
number = {1},
pages = {1-6},
doi = {10.11648/j.ijssam.20251001.11},
url = {https://doi.org/10.11648/j.ijssam.20251001.11},
eprint = {https://article.sciencepublishinggroup.com/pdf/10.11648.j.ijssam.20251001.11},
abstract = {This paper considers the ergodicity of maps on the two-dimensional torus, focusing on transformations where invariant real-valued functions are constant. The study considers both additive and multiplicative transformations, providing a detailed analysis of the conditions required for a map to be classified as ergodic. The investigation is grounded in the theory of dynamical systems and leverages mathematical tools such as orthonormal double sequences in Hilbert spaces and Fourier series to establish necessary and sufficient conditions for ergodicity. By connecting these conditions to the Lebesgue measure, the research outlines the fundamental properties of ergodic transformations on the torus. A key aspect of this study is its treatment of invariant functions and their role in defining ergodic behavior. Invariant functions, which remain unchanged under the dynamics of a given transformation, are examined in depth to understand how their constancy relates to the overall system. The analysis also highlights the interplay between additive and multiplicative transformations and their impact on the ergodic properties of the system. The results of this work not only provide a robust framework for understanding the dynamics of transformations on the two-dimensional torus but also have implications for higher-dimensional systems. This contribution is particularly relevant for studying complex systems in ergodic theory, where the behavior of transformations under the Lebesgue measure often serves as a foundation for further exploration. By addressing these fundamental aspects, the paper lays the groundwork for extending these concepts to more intricate and multidimensional settings in mathematical and applied research.
},
year = {2025}
}
TY - JOUR T1 - Ergodicity of Maps on the Two-Dimensional Torus AU - George Smart Nduka AU - Henry Etaroghene Egbogho Y1 - 2025/02/10 PY - 2025 N1 - https://doi.org/10.11648/j.ijssam.20251001.11 DO - 10.11648/j.ijssam.20251001.11 T2 - International Journal of Systems Science and Applied Mathematics JF - International Journal of Systems Science and Applied Mathematics JO - International Journal of Systems Science and Applied Mathematics SP - 1 EP - 6 PB - Science Publishing Group SN - 2575-5803 UR - https://doi.org/10.11648/j.ijssam.20251001.11 AB - This paper considers the ergodicity of maps on the two-dimensional torus, focusing on transformations where invariant real-valued functions are constant. The study considers both additive and multiplicative transformations, providing a detailed analysis of the conditions required for a map to be classified as ergodic. The investigation is grounded in the theory of dynamical systems and leverages mathematical tools such as orthonormal double sequences in Hilbert spaces and Fourier series to establish necessary and sufficient conditions for ergodicity. By connecting these conditions to the Lebesgue measure, the research outlines the fundamental properties of ergodic transformations on the torus. A key aspect of this study is its treatment of invariant functions and their role in defining ergodic behavior. Invariant functions, which remain unchanged under the dynamics of a given transformation, are examined in depth to understand how their constancy relates to the overall system. The analysis also highlights the interplay between additive and multiplicative transformations and their impact on the ergodic properties of the system. The results of this work not only provide a robust framework for understanding the dynamics of transformations on the two-dimensional torus but also have implications for higher-dimensional systems. This contribution is particularly relevant for studying complex systems in ergodic theory, where the behavior of transformations under the Lebesgue measure often serves as a foundation for further exploration. By addressing these fundamental aspects, the paper lays the groundwork for extending these concepts to more intricate and multidimensional settings in mathematical and applied research. VL - 10 IS - 1 ER -